En esta entrada vamos a enunciar el teorema de Rouché-Frobenius y a ver tres ejemplos de su aplicación.
CLASIFICACIÓN DE UN SISTEMA
Los sitemas de ecuaciones se clasifican según el número de soluciones en
- Sistema incompatible: no tiene solución.
- Sistema compatible determinado: tiene una única solución.
- Sistema compatible indeterminado: tiene infinitas soluciones.
Como el teorema utiliza las matrices asociadas al sistema de ecuaciones, vamos a recordarlas mediante un ejemplo.
EJEMPLO DE LAS MATRICES DE UN SISTEMA
Sea el sistema de ecuaciones lineales
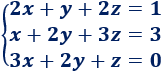
Observad que el orden de aparición de las incógnitas es el mismo en todas las ecuaciones (xx, yy, zz).
Como el sistema tiene 3 ecuaciones y 3 incógnitas, la matriz de coeficientes AA tiene dimensión 3×3. Contiene en la fila mm y columna nn el coeficiente de la incógnita de la posición nn en la ecuación mm:

La matriz de términos independientes, bb, es la columna formada por los números del lado derecho del signo de igualdad de las ecuaciones:

La matriz ampliada, aumentada o completa del sistema, A∗A∗, está formada por la matriz AA y la matriz bb:

Además de esto, necesitamos calcular el rango de una matriz:
RANGO
El rango de una matriz es la mayor dimensión de los menores no nulos de la matriz, o bien, si la matriz está en su forma escalonada (o escalonada reducida), el rango es el número de filas de la matriz menos el número de filas nulas.
Más información: Determinante, rango y menores.
TEOREMA DE ROUCHÉ-FROBENIUS
Sea A⋅x=bA·x=b la representación matricial de un sistema de mm ecuaciones lineales con nn incógnitas. Entonces,
- El sistema es incompatible si el rango de la matriz de coeficientes AA es distinto del rango de la matriz ampliada (A|b)(A|b).
- El sistema es compatible si los rangos coinciden. En este caso, si el rango es igual al número de incógnitas (es decir, nn), el sistema es determinado. Si es menor que nn, es indeterminado.
EJEMPLOS DE APLICACIÓN DEL TEOREMA
En los ejemplos tenemos que calcular el rango de las matrices. Para variar, lo calcularemos de forma distinta en las ejemplos. Más información sobre el rango: Determinante, rango y menores de una matriz.
SISTEMA 1

SISTEMA 2

SISTEMA 3
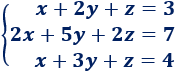

No hay comentarios:
Publicar un comentario